PLDS Switched Control Tutorial #
This tutorial shows how to use this library to control a system with a switched PLDS controller (lds::poisson::SwitchedController). This type of controller is applicable in scenarios where a physical system is not accurately captured by a single LDS but has multiple discrete operating modes where the dynamics can be well-approximated as linear.
In the example that follows, another PLDS model (lds::poisson::System) is used in place of a physical system. It receives control inputs and provides measurements for the simulated feedback control loop. This system stochastically flips between two input gains. Here, the controller is assumed to have a perfect model of the switching system being controlled. Note that in practice, users would need to have a decoder that estimates operating mode of the physical system being controlled. This library does not currently include operating mode estimation.
The full code for this can be found here.
Preamble #
In addition to including the main ldsCtrlEst header, this tutorial will use some shorthand.
#include <ldsCtrlEst>
using lds::Matrix;
using lds::Vector;
using lds::data_t;
using std::cout;
Note that lds::Matrix and lds::Vector are typedefs for arma::Mat<data_t> and arma::Col<data_t>, where the data type is double by default. May be changed to float in include/ldsCtrlEst_h/lds.h if there are memory constraints (e.g., large-scale MIMO control problems).
Creating the simulated system #
A first-order single-input/single-output system will be used for the purposes of this demonstration. The simulation will be run at 1 kHz for 30 seconds.
// whether to do switched control
bool do_switch_ctrl = true;
// Make SISO system sampled at 1kHz
data_t dt = 1e-3;
size_t n_u = 1;
size_t n_x = 1;
size_t n_y = 1;
// no time steps for simulation.
auto n_t = static_cast<size_t>(30.0 / dt);
The system’s input matrix (B) will be switched stochastically from one value (b1) to a less sensitive value (b2) according to the following probabilities.
// for simulating switching
size_t which_mode = 1;
data_t pr_21 = 1e-3; // prob mode 1 -> 2
data_t pr_12 = pr_21; // prob mode 2 -> 1
Initially, the system will be in “mode” 1, where B = b1.
// simulated system being controlled
lds::poisson::System controlled_system(n_u, n_x, n_y, dt);
// **Assume the system is not well characterized by one LDS, but is well
// characterized by two LDS models with different input matrices.**
data_t scale_sys_b = 2;
Matrix a(n_x, n_x, arma::fill::eye);
a[0] = 0.985;
Matrix b1 = Matrix(n_x, n_u).fill(0.05);
Vector d = Vector(n_y, arma::fill::zeros).fill(log(1 * dt));
controlled_system.set_A(a);
controlled_system.set_B(b1);
controlled_system.set_d(d);
controlled_system.Reset(); // reset to initial conditions
See the GLDS Control and PLDS State Estimation tutorials for more detail about creating System objects.
Creating the controller #
Now, create the controller. A switched-system controller (SwitchedController) essentially toggles between the parameters of its subsystems when the controller is told a switch has occured. The first thing the user needs to do is define these subsystems. In this example, there are two Poisson systems (sys1, sys2), which are the same save for their input gains.
Similar to a non-switched controller, constructing a SwitchedController requires these system models and upper/lower bounds on control. See the GLDS Control tutorial for more details. In the case of a SwitchedController, it needs a list of systems, using the std::vector container.
Moreover, when assigning control-related signals such as the feedback controller gains, it is crucial that the list of gains optimized for each operating mode of the system have the same dimensionality. For this reason, this library provides UniformMatrixList and UniformVectorList containers that should be used when setting Kc, Kc_inty, g_design. These containers are std::vectors whose contents are uniformly sized.
Putting this information together, here is how to create the controller and the list of controller gains optimized for each system operating mode.
// create switched controller
lds::poisson::SwitchedController switched_controller;
lds::UniformMatrixList<> k_x; // feedback controller gains
{
// create switched controller sub-systems
// system 1
lds::poisson::System sys1(controlled_system);
// set process noise covariance
Matrix q_controller = Matrix(n_x, n_x, arma::fill::eye) * 5e-3;
sys1.set_Q(q_controller);
// adaptively estimate process disturbance (m)
// n.b. using arbitrary default value for process noise if enabled.
sys1.do_adapt_m = true;
// setting initial mode to target to avoid large error at onset:
Vector x0_controller = arma::log(y_ref0) - d;
sys1.set_x0(x0_controller);
sys1.Reset(); // reset to initial conditions
// system 2
lds::poisson::System sys2 = sys1;
// set parameters
sys2.set_B(b2);
lds::UniformSystemList<lds::poisson::System> systems({sys1, sys2});
// controller gains for underlying systems:
Matrix k_x1(n_u, n_x, arma::fill::ones);
Matrix k_x2 = scale_sys_b * k_x1; // system2 is x-times less sensitive.
k_x = lds::UniformMatrixList<>({k_x1, k_x2});
data_t u_lb = 0.0;
data_t u_ub = 5.0;
switched_controller = std::move(
lds::poisson::SwitchedController(std::move(systems), u_lb, u_ub));
}
Note that the above code block demonstrates how move semantics can be used for assignment/construction. Copy assignment/construction is of course also allowed.
Now that the SwitchedController is instantiated, assign its parameters.
// Control variables
size_t control_type = 0; // no integral action, etc
switched_controller.set_control_type(control_type);
switched_controller.set_Kc(std::move(k_x));
switched_controller.set_y_ref(y_ref0);
Simulating control #
In this demonstration, we will use the ControlOutputReference method which allows users to simply set the reference output event rate (y_ref) and supply the current measurement z. It then calculates the solution for the state/input required to track that output at steady state. In this case, the goal is to regulate the output about a constant reference, so it is appropriate here. This method can also be used for time-varying references as long as this variation is slow compared to the dynamics of the system. Importantly, this method performs control in the linear state space (i.e., taking the logarithm of the reference output).
The control loop is carried out here in a simple for-loop, controlled system is simulated along with stochastic mode switches, a measurement taken, and the control signal updated.
// Let the controlled system stochastically change gain
// Assume another algorithm decodes this mode change and signals the
// switched_controller
Vector chance(1, arma::fill::randu);
if (which_mode == 1) // mode1
{
if (chance[0] < pr_21) {
which_mode = 2;
controlled_system.set_B(b2);
if (do_switch_ctrl) {
switched_controller.Switch(1);
}
}
} else { // mode2
if (chance[0] < pr_12) {
which_mode = 1;
controlled_system.set_B(b1);
if (do_switch_ctrl) {
switched_controller.Switch(0);
}
}
}
// Simulate the true system.
z.col(t) = controlled_system.Simulate(u.col(t - 1));
// perform control
u.col(t) = switched_controller.ControlOutputReference(z.col(t));
Note that as the gain of the controlled system changes stochastically, the controller is informed of this change. In practice, a user must decode such changes in the system’s operating mode and call the Switch method accordingly. Such a decoder is not currently included in this library.
Example simulation result #
Below are example results for this simulation, including outputs, latent states, mode switches, and the control signal. The controller’s online estimates of the output and state are shown in purple.
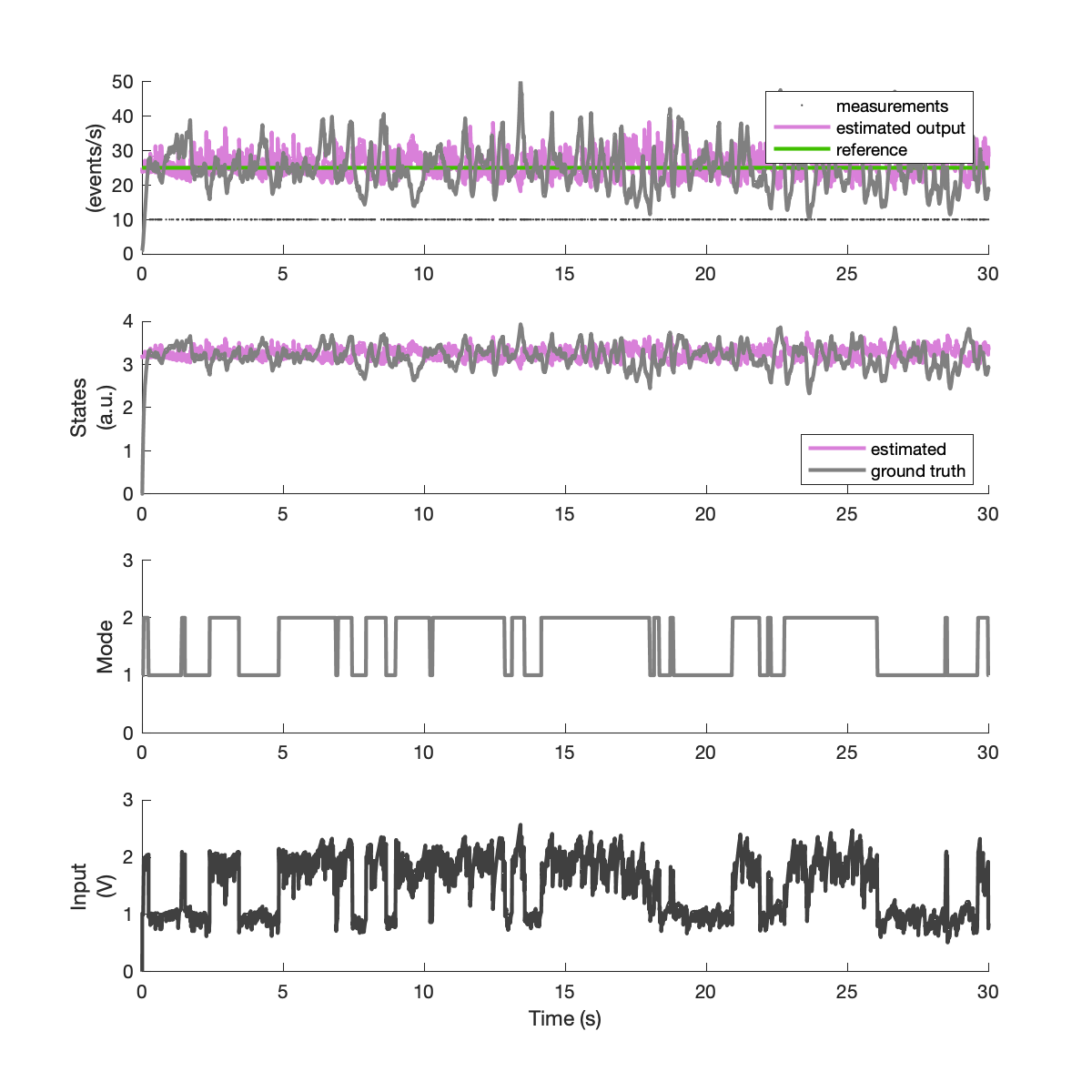
Note that every time the operating mode of the system changes (here, a gain changes), the controller immediately adjusts its inputs. In contrast, a non-switched controller with integral action would also compensate but do so in a comparitively sluggish fashion.